Un petit modèle probabiliste

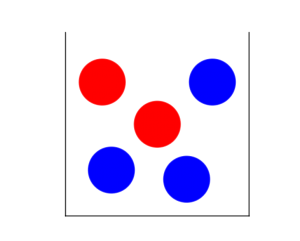
L’urne de Polya est un modèle jouet probabiliste très populaire. Prenez une urne dans laquelle se trouve N boules: r(0) rouges et  b(0) bleus soit r(0)+b(0)=N. On en tire une aléatoirement (uniformément) et on note sa couleur. On replace alors la boule dans l’urne et on y ajoute en plus une autre boule de cette même couleur. Par exemple pour le premier tirage on a la probabilité r(0)/(r(0)+b(0)) d’obtenir une boule rouge. Si on tire effectivement une boule rouge, au deuxième tirage il y aura alors dans l’urne N+1 boules dont r(1)=r(0)+1 rouges et b(1)=b(0) bleus. Puis on recommence ainsi autant de fois qu’on le souhaite (après le n-ième tirage, on a donc r(n) rouges et b(n) bleus avec r(n)+b(n)=N+n).

Qu’est ce que ça donne la limite n tend vers l’infini? Y a t-il (avec grande probabilité) une couleur très majoritaire? C’est à dire b(n)/(r(n)+b(n) ou r(n)/r(n)+b(n)converge vers 0? Ou bien les deux couleurs s’équilibrent-elles et on a b(n)/r(n)+b(n) converge 1/2?
La réponse assez surprenante est ni l’une ni l’autre. On a que presque surement il existe X tel que b(n)/r(n)+b(n) converge vers X mais X est aléatoire sur le segment [0,1]. On peut par ailleurs montrer que X suit une loi bêta B(r(0),b(0)). En particulier si il n’y a au départ une seule boule rouge et une seule boule bleu, X sera équidistribué sur [0,1].

preuve:

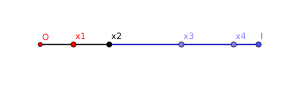
Plaçons nous sur le segment [0,1] et tirons N-1 points aléatoirement indépendamment et identiquement distribués que l’on ordonne 0 < x(1) < x(2) < … x(N-1)<1. Fixons le point x(r(0)). On appellera [0,x(r(0))[ la zone rouge et ]x(r(0)),1] la zone bleu. On dira ensuite que  0,x(1),…,x(r(0)-1) sont rouges et que x(r(0)+1),…,1 sont bleus. Continuons
le tirage de points aléatoire iid uniforme sur [0,1] en fonction de zone où il apparait, il est soit rouge soit bleu. Connaissant x(r(0)) on a une Bernoulli : le point est rouge avec probabilité x(r(0)) et le point est bleu avec proba 1-x(r(0))). La loi des grands nombre
nous dit alors que le nombre moyen de point rouge converge vers x(r(0)). Et on connait également la loi de x(r(0)): c’est une loi bêta B(r(0),b(0)) (Remarquez puisqu’il y a au départ r(0)-1 points sur [0,x(r(0))[ et b(0)-1 points sur ]x(r(0)),1] la fonction de densité
est alors proportionnel à  x(r(0)) puissance r(0)-1 fois (1-x(r(0)) puissance b(0)-1).

Oublions maintenant que l’on connaisse x(r(0)) mais que l’on sait combien de points sont tombés dans la zone rouge (resp bleu). Par définition, après le n-ième tirage x(r(0)) est alors le r(n) plus grand point parmi les N-1+n tirés. Tirons alors un nouveau
point. Puisque que tous les tirages sont iid, tous les ordres possibles des différents points sont équiprobable. En particulier ce nouveau point aura r(n)/(b(n)+r(n)) d’avoir un rang plus petit ou égale que r(n) et b(n)/b(n)+r(n)) d’avoir un rang plus grand que r(n). Et on retrouve alors exactement l’urne de Polya! Elle est donc bien équivalente au tirage de Bernoulli iid que l’on vient de décrire.

Le théorème de De Finetti

L’urne de Polya est probablement l’exemple le plus célèbre d’application du théorème de De Finetti. Pouvoir se ramener à des variable iid est extrêmement intéressant mathématiquement parlant. On souhaiterait savoir quand cela est-il possible. Plus précisément à partir d’une suite de tirages non indépendent, est on capable de décomposer la loi de ces tirages en une variable aléatoire d’environnement (notre
x(r(0))) et que conditionnellement à cette variable les tirages soient indépendants (selon une loi qui dépend de l’environnement x(r(0))). On peut facilement voir que si cela était vrai, alors les lois des tirages aléatoires ne dépendraient pas de l’ordre de la réalisation
du tirage en question. Ceci donne donc une condition nécessaire. Le théorème de De Finetti affirme que cette condition est également suffisante si l’on considère un tirage infini (la proba ne dépend pas d’une permutation finie.). Il s’énonce ainsi pour des Bernoulli:

« Soit X(1),X(2),… une suite infini de variable aléatoire de Bernoulli dont la loi de l’ensemble est invariante par permutation finie. Alors il existe une variable aléatoire Y tel que (X(1)+…+X(n)/n converge vers Y presque surement. De plus conditionnellement à cette limite les variables X(i) se comportent comme des variables de Bernoulli indépendantes et identiquement distribuées avec P(X=1|Y=y)=y et P(X=0|Y=y)=1-y. »

Un sujet de recherche actuel: les marches aléatoires renforcées.

Les marches aléatoires sont omniprésentes chez les probabilistes. Un modèle qui retient l’attention de plusieurs groupes de chercheurs actuellement sont les marches aléatoires renforcées (MAR). C’est à dire des marches aléatoires qui ont plus de chance de retourner à un endroit où elles sont déjà passées avant. Plus précisement, on pose quelque chose comme ça : « Si x est voisin de y (x-y), la probabilité que la marche saute de X(n)=x en X(n+1)=y est de la forme (a+n(y))/S où n(y) est le nombre de fois que la marche a visité y, et S est la somme des (a+n(y’)) sur les voisin de x.

Il se trouve que l’on peut appliquer une variante du théorème de De Finetti dans ce cas ci. Pour chaque sommet, on compte le nombre de fois que la marche a visité chacun de ses voisins et cela se comporte alors comme une sorte d’urne de Polya. On pourra alors construire un environnement aléatoire sur lequel est définit un processus de
Markov qui a la même loi que la MAR. Mais quel est cet environnement aléatoire? La marche reste-elle coincée infinitésiment ou part-elle à l’infini? Et plein d’autres questions sur lesquelles travailler…