Un très beau résultat en géométrie différentielle et que j’aime beaucoup est le théorème de Gauss Bonnet qui s’énonce ainsi: « Pour toute surface S fermée, l’intégrale de sa courbure K est égale à 2 pi fois sa caractéristique d’Euler (nombre de faces – nombre d’arêtes + nombre de sommets)

Ici nous présentons une version un peu simplifiée du théorème de Gauss Bonnet dont l’énoncé et la preuve sont élémentaires. Ils peuvent être présentés à des élèves de collège ou de lycée et donc constitue à mes yeux un sujet parfait pour un exposé de vulgarisation mathématique.

Un petit résultat intermédiaire

Pour un polygone à N cotés la somme des angles vaut (N-2) fois pi. En effet faisons le tour de ce polygone dans le sens des aiguilles d’une montre. Après un tour complet la somme des tournants t(i) vaut toujours 2 pi ceci quelque soit le nombre de tournants réalisés. L’angle a(i) de chaque sommet est égale à pi moins t(i) et on a donc la somme des a(i) est égale à N*pi moins la somme des t(i) soit N*pi-2*pi. Cet exemple n’est pas anodin, car les tournants sont l’équivalent de la courbure en dimension 1.

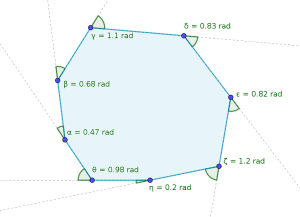
Les coins alias les défauts d’angles

Considérons maintenant des polyèdre en 3 dimensions. Peut-on définir sur ses sommets une notion de coin? Quelque chose d’équivalent aux angles en 2 dimension et qui mesure de combien le sommet est pointu? Une réponse fut proposée par Descartes. Pour un sommet A, on considère les faces f du polyèdre adjacente à A et leur angle a(f) en ce sommet. On définit alors le coin c(A) (disons aussi le défaut d’angle) comme 2*pi moins la somme de ces angles a(f).

Exemples

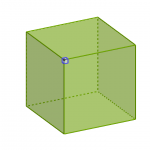
• Pour un cube, Les trois angles valent pi/2 et donc c(A)=2*pi-3*pi/2=pi/2.
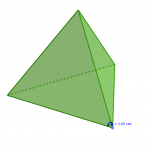
• Pour un tétraèdre régulier : les trois angles valent pi/3, et donc c(A)=2*pi-3*pi/3=pi.

 

Remarquez qu’il peut y avoir des coins négatifs. Cependant cela ne dépend pas si le coin est s’enfonce ou non dans la figure. Par exemple le coin ci dessous est bien positif. Pour voir si un coin est positif ou négatif on déplie le patron de la figure. Si sur le patron les faces autour du sommet ne se recouvrent pas alors la somme des angles est inférieur à 2 pi et au contraire si elles se recouvrent alors elle est supérieur à 2*pi.

 

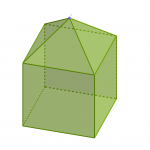
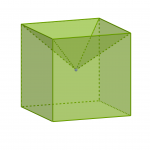
Les coins et la caractéristique d’Euler

Quand est il de la somme des coins du polyèdre? On peut reprendre les exemples précédents:

• Pour le cube, on a 8 sommets, chacun d’un coin égale à pi/2, la somme des coins vaut alors 8*pi/2=4*pi
• Pour le tétraèdre, on a 4 sommets dont chacun a un coin égale à
  pi et donc la somme vaut 4*pi.

Remarquez que l’on retrouve bien à chaque fois la surface de la sphère. On peut montrer ce théorème de Gauss Bonnet simplifié :

Soit un polyèdre P, alors la somme de ses coins est égale à 2*pi fois sa caractéristique d’euler.

PREUVE:

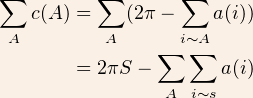
Le deuxième terme est la somme de tous les angles du polyèdre, c’est donc aussi la somme sur toutes les faces f de la somme des angles de cette face et alors:

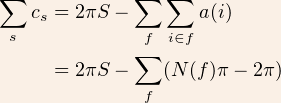
avec N(f) le nombre de cotés de la face f. Dans cette somme chaque arête du polyèdre est comptée 2 fois, et elle est donc égale à 2*A  (A le nombre d’arête du polyèdre). Et on peut conclure : la somme des coins vaut bien 2*pi*(F-A+S).

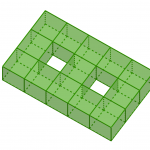
Des surfaces avec trous et sans trous

La caractéristique d’Euler est un des invariants topologique les plus connus, elle permet notamment de classifier les surfaces de dimension 2. Remarquez que pour les polyèdres, la caractéristique d’Euler est bien invariante si on les complexifie en découpant les faces, en ajoutant des sommets ou en déformant la figure. On peut énoncer le résultat suivant : la somme des coins d’un solide (sans trou) vaut toujours 4*pi. Dans le cas général la caractéristique d’Euler vaut 2 moins 2 fois le nombre de « trous ».

Par exemple sur les figures suivantes la somme des coins est égale à 0 et -4*pi:

 

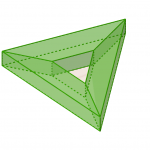
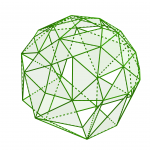
Vers la version continue? Considérons une surface lisse. On peut tout à fait l’approximer par un polyèdre ayant de plus en plus de faces. La somme des coins se comporte alors comme une somme de Riemann qui converge vers l’intégrale de la courbure.

 …  … …  

(somme des coins = intégrale de la courbure = 4*pi)

Et le théorème remarquable de Gauss?}

Il est difficile de parler de Gauss et de courbure sans mentionner le « Theorema egregium » (théorème remarquable) qui affirme que la courbure est invariante par isométrie locale. Énonçons en une variante (très) simplifiée pour les coins :

Soit un polyèdre P qui ne possède que des faces triangulaires, Tout transformation en un polyèdre P’ qui conserve les longueurs des arêtes conserve également la valeur des coins.

La preuve est élémentaire: les longueurs sont conservées, donc les
angles des triangles sont conservés donc par définition les coins
sont conservés.
Par exemple les deux figures précédentes avec le coins qui s’enfonce dans le cube ont les mêmes coins.