Je présente ici une idée très jolie signée Adi Shamir (le “S” dans “RSA”). Celle ci a déjà fait l’objet d’un article sur le site d’Images des Maths et comme elle est superbe je me permet de la réexpliquer ici.
Un groupe et un coffre fort
Un groupe de personnes partage un coffre fort (avec codes à chiffre) et décide d’organiser ensemble la sécurité. Le premier membre propose de simplement donner le code à chacun. Mais le reste du groupe n’est pas d’accord car la sécurité ne serait alors pas très élevée. Il suffit d’un membre soit malhonnête pour que tout soit compromis. Le deuxième membre propose de diviser la clef de sécurité en morceau et d’en donner un à chacun à la même manière des pirates découpant une carte au trésor. La seule façon d’ouvrir le coffre est alors que le groupe tout entier se réunisse. Mais cette idée est également rejetée car contre trop contraignante. Si un membre n’est plus là ou si il a oublié son code, le contenu du coffre est perdu. Un troisième membre ne propose pas de solution mais fait alors remarquer que plusieurs personnes du groupe (mais on ignore lesquelles mais moins que (k-1)) se mettraient volontiers ensemble pour partager leurs informations et ouvrir le coffre au détriment du reste du groupe.
Tout le monde se met alors d’accord sur le cahier des charges suivant:
Si au moins k membres du groupe se réunissent ils doivent toujours être capables d’ouvrir le coffre mais si il n’y a seulement que (k-1) personnes, alors il doit leur être impossible de deviner la combinaison.”
La difficulté ici est qu’il faut ces conditions doivent être valides quelques soient les sous ensembles de k ou (k-1) personnes. Une solution très élégante utilise de l’algèbre linéaire et je la présente maintenant.
Un simple système linéaire
Soit une famille de n vecteurs de dimension k : (a1,…,an) telle que pour toute sous famille de k vecteurs forme une base. Le code consiste maintenant en un vecteur c de de dimension k. À la i-ème personne du groupe on donne comme information le vecteur ai et le réel bi = (ai,c). Pourquoi cela fonctionne ? Pour tout sous ensemble L on a un système avec |L| équations dont l’ensemble des solutions est un espace affine de dimension k-|L| et qui admet donc une infinité de solution pour |L|<k. Par contre avec k personnes il suffit de résoudre (par exemple avec le pivot de Gauss) un système à k équations et k inconnus dont, avec la propriété des (ai), admet une unique solution.
Voici un exemple avec groupe de n=5 personnes A,B,C,D et E et k=3.
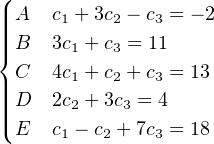
Si on suppose que B,C et E se réunissent, ils obtiennent ensemble le système suivant qu’ils peuvent facilement résoudre.
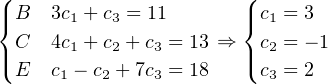
Mais bien sur avec seulement les équations de B et C ou seulement celles de C et E, le système admettrait une infinité de solution.
Il reste la question de comment construire une telle famille de vecteurs ai.
Une première méthode un peu bête mais très efficace et de simplement tirer des vecteurs aux hasards. Puisque sur l’ensemble des matrices k par k, det = 0 est une sous variété de dimension inférieur, la probabilité de toucher cet espace est nulle avec une probabilité continu.
Une deuxième méthode (et celle proposée initialement) et de se placer dans l’espace des polynômes de degré k-1. Le code consiste en les coefficients d’un polynôme P et on donne comme information à chacun « (x,P(x)) » pour des valeurs x différents. Si on revient à notre exemple à 5 personnes, on pourrait avoir
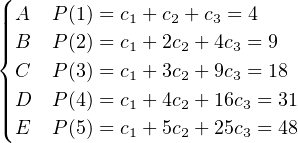Ceci satisfait les conditions du problème car le déterminant de Vandermond est non nul dès que les x sont différents. Ici résoudre le système est également facile en utilisant les polynômes d’interpolation de Lagrange.