La dérivée extérieure
La propriété la plus remarquable de la dérivée extérieure est sans aucun doute le théorème de Stokes :
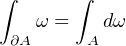
”l’intégrale de la forme différentielle sur le bord de la sous variété est égale à l’intégrale de sa dérivée extérieure sur l’intérieur de cette sous variété”. Cela pourrait même être la définition de la dérivée extérieure et celle ci a l’avantage de donner immédiatement l’intuition et la motivation de cette notion. De même que pour la notion “vitesse” la définition intuitive serait “la quantité qui intégré sur le temps donne la distance parcourue”, pour la dérivé extérieure dω on aurait “la forme différentielle de degré supérieur qui satisfait le théorème de Stokes”. Malheureusement si il est clair que la dérivée extérieure est une notion naturelle et centrale en analyse, que ce soit en physique, en géoscience, en analyse numérique et dans pleins d’autres domaines, on manipule constamment des champs de vecteurs sur des variétés en ne les traitant que comme un ensemble de fonctions réelles sans se poser la question de leurs natures mathématiques. Je trouve donc dommage d’ignorer au passages des très belles notions de géométrie différentielle ou topologie algébrique.
Le but de ce poste est d’écrire toute la théorie de Maxwell avec des dérivées extérieurs. Outre le fait que cette construction est extrêmement élégante. Elle illustre le fait que les formes différentielles et la dérivée extérieure (et la cohomologie de De Rham) sont naturelles et devraient être utilisées plus souvent.
Pour rappel : soit M une variété de dimension n . L’algèbre des formes différentielles Λ(M) est une algèbre graduée où la dérivée extérieure d va des k-formes différentielles au (k+1)-formes différentielles
Ces espaces pouvant aussi être vu comme un champs de vecteurs de dimension k parmi n. La propriété algébrique principale est sans aucun doute d○d=0 : Pour tout espace des k -formes, l’image de d est incluse dans le noyau de d . En un mot, tout le jeu de la cohomologie de De Rham est de comprendre quand a t-on l’égalité entre l’image et le noyau et plus généralement quel est l’espace “manquant”.
La cohomologie de De Rham pour l’espace en trois dimension
Commençons par le cas simple de l’espace en trois dimension, la différentielle extérieure est bien connu mais sous des noms différents de gradient, divergence ou rotationnel:

Remarque: les dimension des espaces sont respectivement 1,3,3 et 1 . Ici la propriété d ○ d=0 n’est rien d’autre que les relations bien connues rot ○ grad =0 et div ○ rot =0 .
Dans le cas présent la cohomologie de De Rham est très facile car l’espace est homotope à un point:
- pour les 0-formes : Ker ( d ) / Im ( d ) = R , c’est à dire on a grad ( f ) =0 ssi il existe une constante c telle que f =c ,
- pour les 1-formes : Ker ( d ) / Im ( d ) =0 , c’est à dire rot ( u ) =0 ssi il existe une fonction f telle que u= grad ( f ) ,
- pour les 2-formes : Ker ( d ) / Im ( d ) =0 , c’est à dire div ( v ) =0 ssi il existe une 1-forme u telle que v= rot ( u ) ,
- pour les 3-formes Ker ( d ) / Im ( d ) =0 , il existe toujours une solution à div ( v ) =g .
Les équations de Maxwell
La théorie de Maxwell est donnée par le magnifique schéma suivant. Chaque flèche du diagramme n’est rien d’autre que la dérivée extérieure.
Le * ici est pour la dualité. En simplifiant la dualité * transforme les k formes et les n-k formes en remplaçant l’ensembles des coordonnées par celles manquante par exemple x,t devient y,z, z devient x,y,t. Ceci permet aussi de définir la dérivée duale ∂ =*d* allant des k formes au ( k-1 ) formes.
Remarquer que les espaces sont de dimension respectivement 1, 4, 6, 4 et 1 . On a noté ici
- le 4- vecteur (V,A) : le potentiel et le potentiel vecteur,
- Le 4 vecteur (ρ,j) : la densité de charge et de courant,
- Le 6- vecteur ( E,B ) le champs électromagnétique.
Le premier avantage ici est que tout est énoncé à un niveau “géométrie” sans un choix particulier de paramétrage. On n’a donc pas à se préoccuper de changements de base (changement de référentielle pour un physicien, changement de carte pour un mathématicien). En particulier il est clair que les champs électriques et magnétiques sont indissociables. Le deuxième avantage est que les notions de k-forme ne sont pas arbitraires mais au contraire sont tout à fait naturelles d’un point de vu physique: Une densité de charge s’intègre sur un volume (3-forme), le courant de charge s’intègre sur une surface fois un temps (3-forme), le champs magnétique s’intègre sur une surface (2-forme) et le potentiel vecteur s’intègre sur un chemin (1-forme). En mécanique quantique ce dernier est lié à la phase de la fonction d’onde de l’électron
Voici maintenant le sens physique de chacune des dérivées extérieures (chaque flèche) du diagramme:
- C’est ici le choix de Jauge, on peut arbitrairement changer
 sans changer les champs électromagnétiques, en effet ( 3 ) ○ ( 1 ) =0 .
sans changer les champs électromagnétiques, en effet ( 3 ) ○ ( 1 ) =0 .
- Un choix particulier de Jauge est ( 2 ) =0 appelée la Jauge de Lorentz:
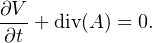 C’est la plus couramment utilisée en électromagnétisme.
C’est la plus couramment utilisée en électromagnétisme.
- On peut exprimer le champs électromagnétisme en fonction du potentiel vecteur :
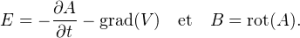
- On a ici les équations de Maxwell-Faraday et Maxwell-Thomson
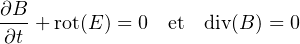 qui découlent bien sur de ( 4 ) ○ ( 3 ) =0 .
qui découlent bien sur de ( 4 ) ○ ( 3 ) =0 .
- C’est maintenant les équations de Maxwell-Gauss et Maxwell-Ampère
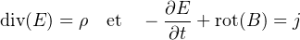
- C’est la loi de conservation de la charge
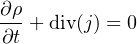 qui est encore ( 6 ) ○ ( 5 ) =0 .
qui est encore ( 6 ) ○ ( 5 ) =0 .
J’en profite pour une petite remarque historique, en 1865 l’idée géniale de Maxwell fut de remarquer que ( 6 ) ○ ( 5 ) ne donnait pas 0 avec l’équation d’Ampère dans la version où elle était énoncée à l’époque. Il la modifia alors en ajoutant le terme dE/dt rendant ainsi la théorie cohérente. Ce sont donc bien des considération de topologie algébrique qui ont mené à la théorie (classique) de l’électromagnétisme telle qu’on la connait aujourd’hui.
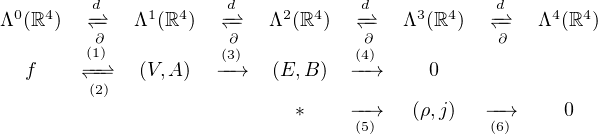
 sans changer les champs électromagnétiques, en effet ( 3 ) ○ ( 1 ) =0 .
sans changer les champs électromagnétiques, en effet ( 3 ) ○ ( 1 ) =0 .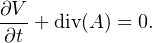 C’est la plus couramment utilisée en électromagnétisme.
C’est la plus couramment utilisée en électromagnétisme.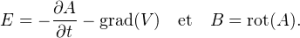
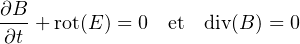 qui découlent bien sur de ( 4 ) ○ ( 3 ) =0 .
qui découlent bien sur de ( 4 ) ○ ( 3 ) =0 .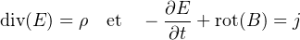
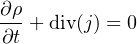 qui est encore ( 6 ) ○ ( 5 ) =0 .
qui est encore ( 6 ) ○ ( 5 ) =0 .