A-Un petit problème du collectionneur (généralisé)
Je souhaiterai apprendre une langue comme le chinois par exemple. Pour cela je procède de la façon suivante. J’ouvre un livre, la radio ou la Télé et au hasard, je choisis un mot que j’écris sur un cahier et je l’append. Puis je recommence plusieurs fois. Si je tombe sur un mot que je connais déjà tant pis, je n’apprend rien de nouveau. Pour ce problème on introduit naturellement la loi de probabilité p(i) sur les mots i qui est la fréquence d’utilisation du mot en question dans la langue courante. Au bout de N (grand) itérations combien de mots ai je appris? Soit S une phrase avec quelle probabilité suis je capable de comprendre tous les mots de S? Combien faut-il d’itérations pour que je connaisse enfin tous les mots (Problème du collectionneur généralisé)?
B-Astuce utilisant la loi de Poisson
Il est possible d’obtenir très facilement une solution en modifions un peu le problème de la manière suivante : on remplace le nombre déterministe N d’itérations par un nombre aléatoire tiré suivant une loi de Poisson de moyenne N. Ce changement ne modifie que très légèrement notre problème puisque l’on va tirer N caractères plus ou moins une erreur d’ordre racine de N (TCL). On utilise alors une propriété extrêmement utile de la loi de Poisson : “Soit P une loi de poisson de paramètre d et X(1),X(2),X(3),… des variables aléatoire discrète sur un ensemble A et indépendantes et identiquement distribuées. Alors les variables
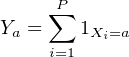
pour a dans A forment une famille de variables aléatoires indépendante qui suivent une loi de Poisson de paramètre d fois Prob(X=a)”. On applique cette propriété à notre problème et on a que pour tout mot i, le nombre de fois que ce mot a été tiré est une loi de Poisson de paramètre Np(i). Je connais donc le mot avec proba 1-exp(-Np(i)). Qui plus est, le tirage de chaque mot est indépendant et donc par exemple je connaitrai la phrase ‘ijk’ avec probabilité [1-exp(-Np(i)][1-exp(-Np(j))][1-exp(-Np(k))] Et pour connaitre tous les mots avec proba
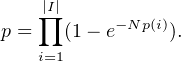
Remarquer que pour p(i)=1/|I| (problème du collectionneur usuel), log(p) vaux environ -|I|exp(-N/|I|) et donc p tend vers 1 si N plus grand que |I|log(|I|) et vers 0 si N plus petit que |I|log(|I|).
Pour un problème d’apprentissage élémentaire par ordinateur, ceci donne un idée grossière du nombre de données à utiliser.
C-Le modèle grand canonique en physique statistique
Le modèle grand canonique, universellement utilisé en physique statistique utilise plus ou moins la même astuce. Plutôt que d’étudier le système avec N particules (modèle canonique) on relâche cette contrainte et on laisse le nombre de particules aléatoire dont la loi est centré autour de N. Par exemple : soit un système ayant k états d’énergie E(1),…,E(k) et N particules. L’énergie total E du système est la somme des E(i)N(i) avec N(i) le nombre de particule dans l’état i. La probabilité de chaque état est proportionnel à ~ e–βE ce qui revient à dire que chaque particule se place en i avec proba
![]()
de manière indépendant. Modifions le système en supposant que le nombre de particules est donné par une loi de Poisson de moyenne N. Alors le nombre de particules dans les états i, deviennent des loi de Poisson indépendantes et de paramètre Np(i) que l’on réécrit souvent introduisant le potentiel chimique eβμ qui vaut
![]()
D-Un petit modèle de serveur
Voici un troisième petit modèle où cette astuce simplifie considérablement de problème.
On dispose d’un arbre binaire de serveurs pour traiter des requêtes. Les requêtes arrivent à la racines. Si il n’y a qu’une requête, le serveur à la racine la traite. Si il y en a plus qu’une le serveur est saturé et ne fait rien. Par contre chaque requête est redirigée vers l’un des deux serveur fils de l’arbre et de manière aléatoire (Bernoulli p=1/2 ) et indépendante. Les deux serveurs fils se comporte alors exactement de la même manière, traitant une requête si elle est seule, ou redirigeant de manière aléatoire les requêtes vers les serveurs suivant dans l’arbre.
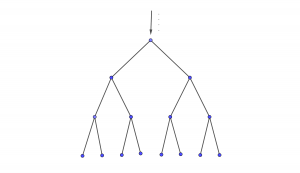
Question : on envoie N requêtes à la racine, quelle profondeur de l’arbre est nécessaire pour traiter ces requêtes.
Réponse : si on remplace le nombre de requêtes à la racine par une loi de poisson de paramètre N, alors après répartition le nombre de requêtes de chaque serveur fils est donné par une loi de Poisson de paramètre N/2 et indépendante. On retrouve ainsi deux copies identiques et indépendantes de notre problème. À la profondeur k il y a 2k copies de Poisson indépendantes de paramètre N∕2k . La probabilité à ce que aucun serveur à cette profondeur n’ai deux requêtes est bornée par 2k (N/2k)2 ce qui donne la profondeur k ≈ 2log2(N).
