Formule de la résolvante

Soit A et B deux matrices, la formule de la résolvante est la relation algébrique suivante

Elle est également valables si A et B sont des opérateurs linéaires sur un espace de dimension infini. Si l’énoncé et la preuve sont élémentaires, cette formule peut se révéler incroyablement utile, en particulier pour faire des développements perturbatifs. On a en effet en réinjectant la formule dans son dernier terme :

et par itération on obtient le développement perturbatif suivant

Je donne ici quelques exemples d’application plus ou moins direct.

Le calcul perturbatif d’une valeur propre

Soit A une matrice ayant une valeur propre simple l(0) et B une autre matrice. On souhaiterai avoir le développement en série entière en t de l(t) la valeur propre
de A+t B. Pour cela on peut utiliser la formule de Cauchy

où on intègre sur un petit cercle dans le plan complexe autour de l(0) et alors, on peut utiliser le développement perturbatif. Par exemple avec A la matrice
diagonal lambda, le terme d’ordre 2 est donné par

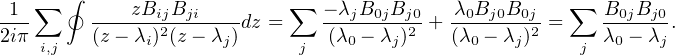
Pour obtenir une formule à un ordre quelconque : EigenvaluePerturbationTheory

Exemple 2 : Une variante du principe Huygens Fresnel.

Une source lumineuse en un point x émet une onde de fréquence w et se propage dans un milieu selon un opérateur H. La lumière F(y) en tout point y est alors donnée par

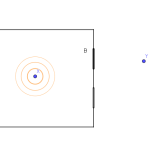
Imaginons que le milieu est composé d’un espace fermé munie d’une ouverture. Dans notre opérateur, H=A si l’ouverture B est fermée et A-B si l’ouverture est ouverte. Lors que l’ouverture est fermée et que y se trouve à l’extérieur par rapport à x aucune lumière n’est reçue. Alors la formule de la résolvante lorsque l’ouverture est ouverte

peut s’interpréter ainsi : « les points z de l’ouverture se comportent comme des sources lumineuses secondaires d’intensité et de phase données par la résolvante lorsque l’ouverture est fermée. »

Exemple 3 : les diagrammes de Feynman.

C’est très certainement l’exemple le plus célèbre et probablement le plus impressionnant d’utilisation de la théorie de perturbation en physique. L’évolution d’un système quantique est décrit par un Hamiltonien H et l’équation de Schrödinger idf(t)=Hf(t)dt qui donne formellement la solution exp(-itH)f(t=0). Il est intéressant d’en étudier la transformé de Fourier (Laplace)

1. La recette pour les diagrammes de Feynman est la suivante: Le Hamiltonien se décompose en un terme d’évolution libre des particules A et un terme d’interaction B qui en théorie quantique des champs s’exprime comme la création et annihilation de particules. On supposera l’interaction B est petit et on fera
   le développement perturbatif.
2. Pour les calculs on travaillera dans la base de Fourier dans laquelle les termes d’évolutions libre A est diagonal. Les termes d’interaction sont ponctuels (local), dans la base de Fourier ils s’expriment sous forme d’intégrale.

Exemple 1: Une désintégration en deux particules

On considère une particule de masse M au repos qui se désintègre en deux particules m1 et m2 de masses plus petites. Le terme d’ordre 1 fait apparaît l’élément

avec a,b,c: les opérateurs de création/annihilation des particules M, m1, et m2 d’impulsion k. Il se dessine avec le diagramme de Feynman suivant

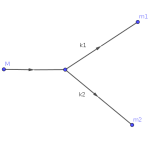
et permet de calculer le taux de désintégration en choisissant z0=M+it.

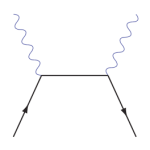
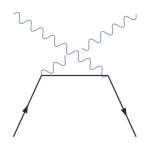
Exemple 2 : La diffusion Compton

La diffusion Compton, c’est le choc entre un électron et un photon. Initialement, on a  un photon d’impulsion k0 et un électron d’impulsion p0. Faire le développement à l’ordre 2 donne 4 termes mais seuls les termes

et

sont pertinents où a et c sont des opérateurs de création/annihilation
de l’électron et du photon. Ils correspondent aux diagrammes de Feynman
suivant