Je présente ici deux petits modèles de théorie des jeux que je trouve intéressant car ils mènent à des conclusions complètement contraire à ce qu’on aurait pu s’attendre à première vu.
Une route trop efficace qui mène à des embouteillages.
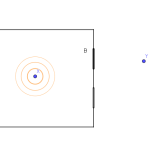
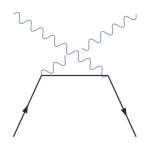
Une ville A est connectée à une ville C par deux routes, celle passant par B et celle passant par D. Chacune est composée de deux tronçons : une partie route de campagne (trait plein) et une partie autoroute (pointillés) comme sur le schéma. Sur la route de campagne la vitesse est limité et le temps pour la parcourir est toujours le même 1 heure. Sur l’autoroute
on peut aller plus vite mais si il y a trop de monde, on doit ralentir à cause des bouchons. Pour la traverser, on met p heure où p entre 0 et 1 est la proportion de personnes circulant sur la route.
Les automobilistes cherchent toujours à mettre le moins de temps possible et choisiront une routes plus rapide si ils en ont l’occasion. Dans la situations présente si une proportion trop importante prennent la route, la deuxième devient plus rapide car moins fréquenté. Des automobilistes changeront alors de trajets les jours suivants. Les
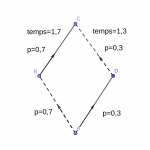
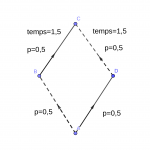
fréquentations s’équilibrent avec la moitié des conducteurs sur chacune des routes. Au finals le temps pour aller de A à C sera 1+0,5=1,5.
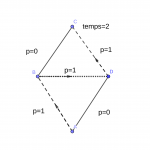
Ajoutons maintenant une super-route entre B et D. Extrêmement rapide et sans bouchons, on peut la parcourir presque instantanément.
Dans cette nouvelle situation, les automobilistes peuvent si ils le souhaitent n’utiliser que des autoroutes et la super route. Comme c’est toujours le choix préférable, personne n’a intérêt à ne pas le faire. Au final tout le monde emprunte les autoroutes. Mais cela
provocant des embouteillages, le temps total est alors 2 heures qui est pire que la situation sans la super route.
Se mettre en difficulté est parfois préférable.
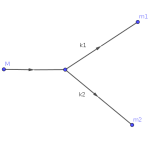
Ici c’est un simple jeux à deux joueurs Valérie et Thomas et qui se joue en un seul tour. Valérie commence et choisit entre deux possibilités a ou b, puis c’est au tour de Thomas de choisir entre deux possibilités X ou Y. C’est fini. Chacun des joueurs gagnent le nombre de point selon le tableau suivant.

Chaque joueur vise le plus de gain possible. Valérie est donc capable de prédire le coup de Thomas. Si elle joue a, Thomas aura intérêt à jouer X. Il gagnera alors 2 points et Valérie 4. Si maintenant Valérie joue b, alors elle doit s’attendre à ce que Thomas joue Y
avec pour résultat 2 point pour Valérie et 5 point pour Thomas. Pour Valérie, la meilleur stratégie est donc de choisir a. Résultat final : (4,2).
Changeons maintenant la grille de la manière suivante.
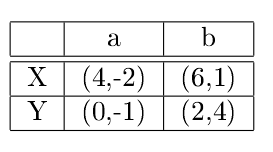
Remarquez que les score de Valérie n’ont pas changés, par contre quelque soit le résultat final Thomas gagne moins de point que la situation précédente.
Reprenons maintenant le jeu: Si Valérie joue a, Thomas choisira Y ce qui n’intéresse pas du tout Valérie. Elle jouera donc b en sachant que Thomas jouera Y. Ici le résultat final est (2,4). Mais alors Thomas gagne plus de points que précédemment.
Conclusion, bien que sur toutes les combinaisons possible le résultat de Thomas est inférieur dans le deuxième jeu que dans le premier, Thomas gagne plus de points dans le deuxième jeu.